1   L’ipotesi del continuo
2   La non contraddittorietà degli enunciati dell’Aritmetica
3   L’uguaglianza in volume di due tetraedri aventi superficie di base ed altezza uguali
4   Il problema della retta come curva di minima distanza tra due punti
5   Il concetto di Lie dei gruppi continui di trasformazioni, senza l’ipotesi della differenziabilità delle funzioni che definiscono i gruppi
6   Trattazione matematica degli assiomi della fisica
7   Irrazionalità e trascendenza di alcuni numeri
8   Problemi sui numeri primi
9   Dimostrazione della più generale legge di reciprocità in un qualsiasi corpo numerico
10 Decisione della risolubilità di una equazione diofantea
11 Forme quadratiche con coefficienti algebrici numerici arbitrari
12 Estensione del teorema di Kronecker sui corpi abeliani, ad un qualsiasi dominio algebrico di razionalità
13 Impossibilità della risoluzione dell’equazione generale di 7° grado mediante funzioni di due soli argomenti
14 Dimostrazione della finitezza di certi sistemi completi di funzioni
15 Fondamenti rigorosi del calcolo enumerativo di Schubert
16 Problema della topologia delle curve e superfici algebriche
17 Espressione di forme definite mediante quadrati
18 Generazione dello spazio a partire da poliedri congruenti
19 Le soluzioni di problemi regolari sul calcolo delle variazioni sono sempre necessariamente analitiche ?
20 Il problema generale dei valori al contorno
21 Dimostrazione dell’esistenza di equazioni differenziali lineari aventi un prescritto gruppo di monodromia
22 Uniformizzazione di relazioni analitiche mediante funzioni automorfe
23 Ulteriori sviluppi dei metodi del calcolo delle variazioni

(dalla conferenza tenuta al Congresso Internazionale dei Matematici. Parigi, la mattina dell’8 agosto 1900)

I problemi di Hilbert: rilevanza storica e metodologica

(da E. Ambrisi e B.Rizzi, I problemi di Hilbert : rilevanza storica e metodologica, in Periodico di Matematiche, n.2/1993)

Premessa
Cosa ci riserva il futuro?
Come prefigurarsi ciò che accadrà domani, fra un anno o più in là?
Riteniamo che questa sia una domanda connaturata all’uomo pensante, qualunque sia l’attività che lo impegna.
Ed è con questo quesito che David Hilbert aprì la sua conferenza “Mathematische Probleme” al secondo congresso internazionale dei matematici a Parigi. Era il 1900: un anno che chiudeva un secolo, a ragione ritenuto aureo per la grande messe di risultati matematici prodotti, ed era l’inizio di un altro le cui aspettative si prefiguravano non meno lusinghiere.

“Chi di noi – iniziò Hilbert – non vorrebbe sollevare il velo sotto cui sta nascosto il futuro, per gettare uno sguardo sui prossimi progressi della nostra scienza e sui segreti del suo sviluppo durante i secoli venturi? Quali saranno gli speciali obiettivi a cui mireranno le più insigni menti matematiche delle generazioni future? Quali nuovi metodi e quali nuovi risultati scopriranno i nuovi secoli, nell’ampio e ricco campo del pensiero umano?”.

A meno di essere dei chiaroveggenti, come fare per vedere nel futuro, quale metodo o calcolo applicare?
L’idea di Hilbert ancora oggi è molto valida proprio perchè pratica e razionale: “Se vogliamo immaginarci lo sviluppo presumibile della conoscenza matematica nel prossimo futuro, dobbiamo far passare davanti alla nostra mente le questioni aperte e dobbiamo considerare i problemi che sono posti dalla scienza attuale e la cui soluzione attendiamo dal futuro. Questi giorni, che stanno a cavallo tra due secoli, mi sembrano ben adatti per una rassegna dei problemi ….”. Si trattava in definitiva di fare il punto della situazione, una completa ricognizione dell’esistente e su questa si sarebbe potuto prevedere ed innestare un programma di attività e di ricerca.

L’idea come è stato detto conserva una sua validità e per molti esperti risulta particolarmente eccitante. Il logico e matematico Hao Wang ad esempio, ha scritto:

“Se un gruppo di persone sufficientemente rappresentativo compilasse una lista di venti o trenta problemi oggi al centro dell’attenzione, si potrebbe adoperarla come base per:

1) raffigurare lo stato attuale della matematica e le relazioni di questa disciplina con le altre scienze;
2) riesaminare la storia;
3) prevedere le tendenze future;
4) individuare un qualche tipo di unità concettuale nel complesso della matematica;
5) discutere alcune delle eterne questioni epistemologiche.
Hilbert operò dunque la sua rassegna di problemi e la lista che ne propose rimane, fino ad ora, un fatto unico, irripetuto e chissà quando e se ripetibile.

La rassegna di Hilbert
I problemi che compongono la rassegna di Hilbert sono 23, e non tutti egli riuscì ad esporre la mattina di quel Mercoledì 8 agosto. Possiamo suddividerli in tre gruppi.

Il primo gruppo, i problemi da 1 a 6, sono di natura fondazionale. Il primo di essi, come è noto, riguarda la ipotesi del continuo; il secondo la non contraddittorietà dell’aritmetica.
Tra le poche osservazioni dei congressisti alla relazione di Hilbert, una riguardava questo secondo problema e fu avanzata da G. Peano il quale obiettò che a parer suo il sistema con le proprietà volute era già stato formulato dai suoi compatrioti Burali-Forti, Padoa e Pieri. Peano dichiarò anche che la relazione di Padoa che sarebbe stata presentata al congresso : Un nuovo sistema di postulati irriducibili per l’algebra avrebbe risposto al problema.

Il terzo e il quarto problema sono di natura geometrica, il quinto è incentrato sul concetto di S.Lie dei gruppi continui di trasformazione, il sesto riguarda la trattazione matematica degli assiomi della fisica e la fondazione assiomatica della probabilità.

Il secondo gruppo di problemi dal 7 al 14, è di natura aritmetica e algebrica. Tra questi i più noti sono il 7 – sulla irrazionalità e trascendenza di alcuni numeri -, l’8 -sui numeri primi e l’ipotesi di Riemann – e il decimo sulla risolubilità di equazioni diofantine.

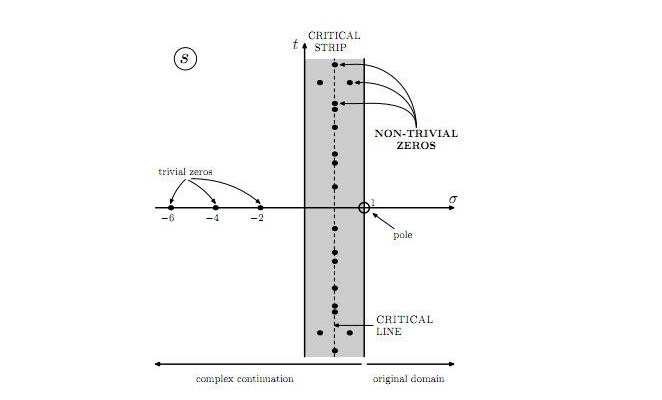
funzione Z di Riemann

Il problema 15 riguarda la fondazione rigorosa del calcolo della numerazione di Schubert e l’ultimo gruppo dal 16 al 23 sostanzialmente la topologia e l’analisi. Si differenzia forse il 18, insieme al 3 e 4, tra i pochi problemi di natura prettamente geometrica e di cui si è recentemente occupata la stampa. Riguarda, questo problema, la distribuzione delle sfere nello spazio.

I problemi 19, 20 e 23 riguardano il calcolo delle variazioni alle cui questioni Hilbert assegnava una grande importanza prevedendone anche una marcata influenza nel successivo sviluppo della ricerca matematica. E così è stato.

Un commento merita pure il problema 22 sulla uniformizzazione di relazioni analitiche mediante funzioni automorfe.
La classica teoria della uniformizzazione, sviluppata principalmente nelle ultime due decadi del XIX secolo e la prima decade del XX secolo, consisteva nel dimostrare che ogni curva, algebrica o analitica, può essere uniformizzata, cioè rappresentata parametricamente da funzioni ad un sol valore o uniformi.

La storia della teoria – a parere di L. Bers – è affascinante prima di tutto per la ricchezza di idee matematiche che ne sono sorte: la dimensione topologica, il ricoprimento dello spazio, le applicazioni conformi e quasi conformi, ecc.
Ma ugualmente affascinante è l’aspetto umano: Schotcky, ad esempio pervenne a congetturare un teorema di uniformizzazione abbastanza generale ma rinunciò ad andare avanti nel suo lavoro per il giudizio non incoraggiante dell’autorevole K.Weierstrass e similmente avvenne per il giovane Poincarè per l’avversione questa volta di F. Klein che per quanto fosse di poco più anziano era già allora all’apice della notorietà e del peso scientifico.
Hilbert ebbe il merito di richiamare l’attenzione verso il problema e fu lo stesso Poincarè, un quarto di secolo dopo il suo primo interesse per la teoria, a risolvere pienamente il problema nella forma posta da Hilbert dividendone però il merito con Koebe.

L’importanza espositiva e didattica
La lista di Hilbert riscontrò un consenso unanime ed enorme fu la sua incidenza: i suoi problemi giocarono il ruolo di grandi problemi, di veri e propri punti di riferimento o mete alle quali il lavoro dei matematici doveva tendere e mirare.

Aprivano dei tracciati e ne illuminavano i percorsi ed è indubbio che ciò giovò alla ricerca scientifica, ad indirizzare i giovani matematici ed anche a rinnovare corsi universitari e con questi anche l’insegnamento della matematica nelle scuole ne trasse grossi benefici.
Di lì a poco molti dei problemi di Hilbert cominciarono ad avere una risposta e i percorsi di ricerca prima illuminati dettero luogo ad itinerari didattici, universitari e secondari, accettati ed universalmente seguiti.
Dal punto di vista espositivo e didattico, si trattò di un avvenimento eccezionale che comportò una precisa organizzazione e sistemazione della matematica anche se questa veniva compiuta in riferimento ai punti terminali cioè ai problemi da risolvere e ai nodi da sciogliere – un analogo di ben definiti e precisati obiettivi educativi e didattici – e non già ai punti di partenza, che pure furono il fondamento delle ricerche di Hilbert e del suo programma formalista.

Furono questi ultimi d’altronde a richiamare molta dell’attenzione del gruppo Bourbaki (per molti versi e a ragione ritenuto continuatore del programma hilbertiano) costituitosi in Francia negli anni 1934/35 nell’intento di costruire non una ma la sistemazione delle matematiche.

Anche Bourbaki ha finito per avere una enorme influenza sul piano dell’educazione matematica sospinto e collaborato dalle ricerche psicologiche di J.Piaget che, in accordo e parallelamente a Bourbaki, vedeva alla base dello sviluppo psicologico del fanciullo le stesse strutture che Bourbaki aveva chiamato “strutture madri” e posto a fondamento della matematica.
Nel loro influsso sulla didattica, Hilbert e Bourbaki-Piaget sono per certi versi complementari: mentre il primo stabilisce le “mete” (che una volta raggiunte scoprono nuovi panorami) che tracciano e illuminano il percorso più adeguato, l’itinerario migliore per arrivarci, il secondo suppone che esistano “punti” da cui tutto ciò che è noto si offre al panorama.

Per quanto riguarda gli effetti, Hilbert ha stabilito un ordine e un itinerario didattico standard, Bourbaki-Piaget ha prodotto una grossa perturbazione in quest’ordine.

Oggi la situazione appare decisamente diversa ed in particolare priva di punti di riferimento.
Non v’è più una teoria degli insiemi ma v’è l’informatica, ed è qualcosa di diverso; non vi sono particolari e nuovi argomenti o capitoli di cui si raccomanda l’importanza e l’inserimento nei programmi ufficiali di studio ma piuttosto e più semplicemente l’esigenza di una maggiore speditezza e significatività nella presentazione della matematica.

Il discorso da interno alla disciplina e sostanzialmente di grossa perturbazione dei curricoli standard o canonici è divenuto più generale, tecnologico e di costume, con particolare attenzione alla sistemazione e alla organizzazione dei concetti e delle procedure ed anche le discussioni sulle geometrie sono mutate: il globalismo del programma di Klein sembra aver lasciato il posto ad una più generale distinzione tra geometria della natura e geometria euclidea che acquista sempre più il carattere, per dirla con Monod, di una geometria teleonomica cioè rispondente ad un progetto, un progetto intellettuale dell’uomo quindi un artefatto cioè etimologicamente un prodotto dell’arte dell’uomo.

I problemi generali
Ma torniamo ad Hilbert.
A conclusione del suo articolo, Hilbert asserisce che i problemi da lui menzionati “sono solo campioni di problemi; ma sono sufficienti a far vedere quanto sia ricca, quanto sia varia, quanto sia estesa oggi la scienza matematica”.
Questa constatazione, questo stato di fatto – alla data del 1900 – lo spinge a sollevare due domande che costituiscono esse stesse due grandi problemi di carattere generale che si può azzardare di chiamare problemi 24 e 25 di Hilbert.

Si chiede Hilbert:
24) non è imminente per la matematica ciò che da tempo è già accaduto per le altre scienze, cioè di dividersi in singole sottoscienze i cui esponenti difficilmente si comprendono ancora tra di loro e le cui connessioni perciò si allentano sempre più?

25) con l’estendersi della scienza matematica non diverrà alla fine impossibile per il singolo ricercatore comprendere tutte le parti?

Quanto sia varia e quanto sia ricca oggi la matematica è certamente lecito chiederselo e alle domande di Hilbert è probabile che non si possa rispondere con il medesimo suo ottimismo con la medesima sua fede sulla risolubilità di ogni problema, sulla inesistenza di un qualsiasi ignorabimus, sulla unità della matematica, quasi una realtà ontologica.
L’analisi è possibile proprio esaminando i tentativi fatti di ripetibilità del lavoro di Hilbert.

La ripetibilità della rassegna
Ci si è interrogati spesso sulla ripetibilità della rassegna operata da Hilbert e abbiamo già riferito di H. Wang. Ma gli esempi sono molteplici.

Recentemente J. Ewing, in occasione di uno dei congressi matematici, ha ripreso la questione esprimendo l’augurio che un matematico o un equipe di matematici ritentasse di realizzare ciò che al merito del solo Hilbert si può finore ascrivere. Ma l’idea di utilizzare la lista di Hilbert quale base per valutare i progressi compiuti dalla matematica nell’arco di più decenni è stata spesso riproposta e a John von Neumann fu esplicitamente chiesto di fornire una lista aggiornata al 1954. Von Neumann, però, declinò l’invito dichiarandosi “incapace di spaziare in un così vasto campo”.

Vent’anni dopo, nel maggio del 1974, l’American Mathematical Society organizzò uno speciale simposio con lo scopo di valutare gli sviluppi e le conseguenze di ognuno dei ventitre problemi posti da Hilbert e allo stesso tempo anche con l’obiettivo di stilare un elenco dei problemi attuali e la consapevolezza della difficoltà dell’operazione è insita nel fatto che per renderla più possibile si restrinse il campo a quei problemi che avessero un legame con i problemi di Hilbert una sorta di filiazione diretta o anche riflessa.

Il lavoro preparatorio di quest’ultimo impegno fu iniziato da J. Dieudonnè e portato a compimento da F.E. Browder attraverso una fittissima corrispondenza con matematici impegnati nei diversi campi di ricerca ed in ogni parte del mondo.

E’ certamente un lavoro molto impegnativo e per quanto condensato in poche pagine, enorme. Il gran numero di matematici impegnati, la loro competenza specifica, le modalità stesse di listare i problemi per settori testimoniano di quanto sia varia e ricca oggi la matematica tanto da non stare più nella mente di una sola persona.
Il prodotto di questo lavoro è una lista di circa 130 problemi suddivisi in 27 branche o aree della matematica e frutto delle risposte di una trentina di specialisti. Frutto del lavoro dunque di più intelletti e non la sintesi elaborata da una mente sola come fu per il lavoro di Hilbert.

E’ dunque necessario riferirsi a problemi più generali e tra questi appare essenziale oggi il problema della comunicazione. E’ lo stesso Wang che inserisce tra i problemi generali che la matematica si trova ad affrontare quello della comunicazione. Esposizione, inserimento, meccanizzazione della matematica – egli dice – sono tra i problemi fondamentali che la matematica si trova ad affrontare. Problemi di comunicazione piuttosto che di ottenimento di nuovi frammenti di matematica. Costituzione ancora di una critica matematica come analogo della critica letteraria.

Questo della comunicazione è un problema molto avvertito e discende anche ed è in accordo alle conclusioni alle quali sono pervenuti molti studiosi di intelligenza artificiale. Il principio enunciato da S. Papert ad esempio, secondo il quale nuovi stadi della conoscenza si raggiungono sfruttando ciò che già si sa o le risultanze del lavoro di M.Minsky per il quale dobbiamo trovare nuove forme di gestione ed amministrazione delle cose note.
L’accordo, cioè, stabilito alcuni decenni fa, tra ricerca matematica e ricerca psico-pedagogica ha trovato oggi un suo rinnovamento per il concorso anche delle indagini e degli studi di intelligenza artificiale.

Oggi si è sostanzialmente d’accordo sul fatto che non basta e non è sufficiente imparare molte cose; occorre, è necessario anche gestire ciò che si impara.
Così tutti gli insegnanti nella loro esperienza sanno di aver compreso perfettamente una cosa nell’atto di spiegarlo a qualcun altro. Esposizione, critica, valutazione sono attività per cervelli mediocri scriveva sul finire della sua carriera, intensamente creativa, il grande G. Hardy; oggi, di contro per il fisico e cosmologo S. Hawking, la spiegazione è il fine ultimo della scienza.

Organizzazione del sapere e spiegazione si presentano cioè come ineludibili problemi attuali non solo della matematica ma dell’intera scienza.
Si colloca qui dunque e si chiarifica il problema dell’insegnamento. Il problema di come insegnare la matematica è più che altro il problema di come ricreare la conoscenza matematica, il sapere matematico e questo intimamente connesso al problema più generale di un impegno collettivo di comunicazione, esposizione, organizzazione. Questo concetto ha origini antiche e si è più volte ripresentato nella storia. Un esempio lo troviamo nelle pagine di uno dei nostri più grandi poeti e prosatori, in G. Leopardi. In una delle sue Operette Morali, il Parini ovvero della Gloria, scrive che ordinariamente si crede che il progresso del sapere dipende dai grossi geni. Certamente il sapere deve molto a questi; ma, contrariamente a ciò che si ritiene, il suo progresso deve meno ai grandi ingegni e molto di più agli ingegni ordinari o anche mediocri i quali riflettendo sulle nuove idee, sui risultati ottenuti dalle grandi menti pian piano li rendono intelligibili a sè e a un più vasto pubblico. E’ in ciò che consiste il progresso del sapere ed è così che esso si realizza perché un nuovo risultato è tale e quando è capito quando è compreso nel suo perché e nel suo significato e, cosa più importante, quando possibile, connetterlo legarlo ad altri risultati.
Sarà così possibile rendere la matematica meno esoterica anche perché il lamento sull’esoterismo della matematica è una tradizione e un abito che occorre smettere.

Il problema dell’insegnamento è dunque il problema fondamentale della matematica, un problema che può giovare anzi è essenziale per lo stesso significato della matematica e per la sua crescita.
Il movimento noto sotto il nome di “movimento per il rinnovamento dell’insegnamento della matematica” fa ormai parte di una letteratura consolidata e passata.

In definitiva questo movimento c’è stato; è un dato di fatto. Non ha interessato solo la scuola ma il sapere e la cultura, i mezzi di comunicazione e i sistemi educativi in generale. Non è durato poco ma, almeno in Italia, se ne è discusso per quasi due decenni e chi vi ha partecipato ha vissuto dell’entusiasmo e dell’ansia innovativa degli anni sessanta e settanta. Si è trattato certo di un momento di eccitazione globale, di un periodo eroico che ha investito e pervaso il mondo dell’insegnamento della matematica. Oggi pure si discute di rinnovamento ma in forma diversa, come è pure giusto che sia. Non v’è più una teoria degli insiemi ma v’è l’informatica, ed è qualcosa di diverso; non vi sono particolari e nuovi argomenti o capitoli di cui si raccomanda l’importanza e l’inserimento nei programmi ufficiali di studio ma piuttosto e più semplicemente l’esigenza di una maggiore speditezza e significatività nella presentazione della matematica. Come prodotto di quel movimento, etichettato della matematica moderna v’è certo, nell’impostazione generale dei processi di riforma attuati in questi anni in Italia, il riconoscimento della centralità didattica della lingua e della matematica. L’augurio è che questa centralità possa essere conservata e rafforzata anche in riferimento agli stimoli provenienti da una nuova matematica moderna.