La matematica del caos: i Frattali

L’avvento delle tecnologie computerizzate ha permesso di visualizzare il comportamento di complesse funzioni matematiche che producono immagini grafiche sorprendenti, che fino a pochi anni fa erano studiate solo teoricamente su fogli di carta quadrettati, senza poter immaginare i segreti e la bellezza mozzafiato di tali rappresentazioni.

Oggi invece utilizzando una workstation grafica sono sufficienti poche frazioni di secondi per visualizzare tali funzioni che producono immagini sorprendenti in termini di particolari e dettagli che ricordano la complessità di forme geometriche ricorrenti in natura (fiocchi di neve, felci, foglie, chiocciole, …)

L’industria del Design e della Moda ha preso in prestito questi concetti matematici per ispirarsi a nuove creazioni, aprendo così nuovi filoni di business.

Uno degli esempi più visibili è rappresentato da un brand emergente della moda internazionale come Desigual che lega il suo stesso logo ai modelli generati dalle funzioni matematiche che rientrano nella categoria dei Frattali:

  (cliccare immagine per miglior risoluzione)

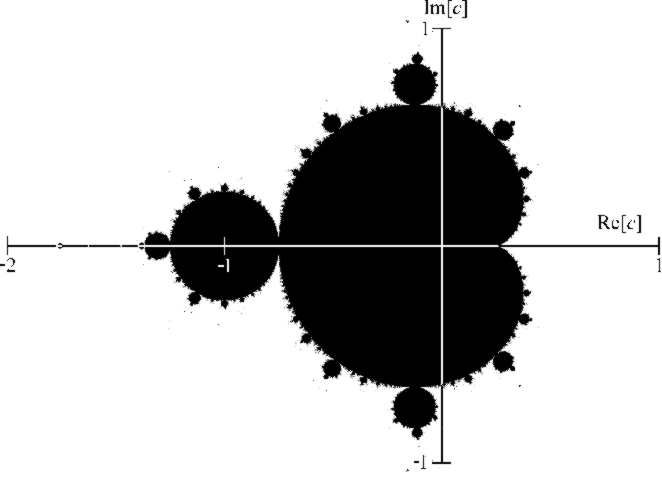
Confrontando il logo stesso dell’azienda con l’immagine matematica seguente, è evidente la somiglianza con la funzione generata dai frattali di Mandelbrot:

Anche alcuni marchi più tradizionali si ispirano per le loro creazioni agli incredibili colori e forme dei Frattali. Ad esempio PIQUADRO, leader nella produzione di borse e valige professionali, ha deciso di dedicare una linea completa, OPERA, ai frattali:

Cosa sono i frattali

Semplificando al massimo il concetto di frattale, lo si può definire come una figura geometrica caratterizzata dal ripetersi sino all’infinito di uno stesso motivo su scala sempre più ridotta.

Intuitivamente un singolo motivo viene ripetuto su scale decrescenti; ingrandendo una parte dell’immagine è possibile individuarvi una copia in scala dell’immagine stessa.

Più formalmente un frattale è dotato di omotetia interna: si ripete nella sua forma allo stesso modo su scale diverse, e dunque ingrandendo una qualunque sua parte si ottiene una figura simile all’originale.

  (cliccare immagine per miglior risoluzione)

Oggi la matematica considera frattale una funzione ricorsiva¹ F i cui valori tendono all’infinito a velocità variabile. La velocità di convergenza all’infinito di F viene rappresentata graficamente con tonalità di colore diverso, mentre con il colore nero si rappresentano i valori finiti della funzione. La funzione F deve avere proprietà simili alle quattro elencate qui di seguito:

1. Autosimilarità: un frattale è unione di copie di se stesso su scale differenti, pertanto la funzione F che genera tale frattale è unione di copie di se stessa su scale differenti.

Da un punto di vista geometrico si consideri un segmento e lo si divida in tre parti uguali, quindi si sostituisca la parte centrale con due segmenti uguali a quello rimosso, in modo da formare un triangolo equilatero

Se si ripete (itera) questa procedura su ognuno dei segmenti, si genera una spezzata sempre più frastagliata, che dà origine ad immagini come le seguenti:

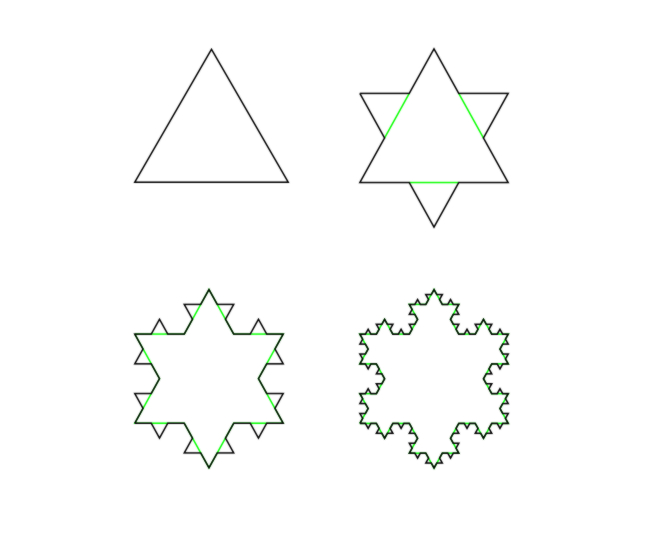
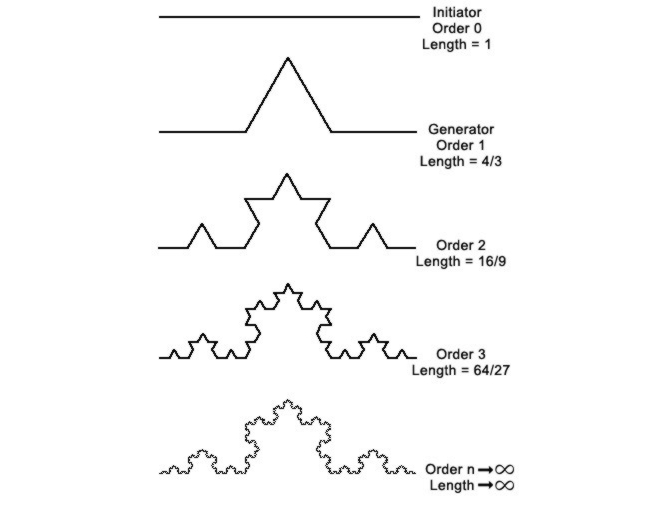
2.  Struttura fine: F rivela dettagli ad ogni ingrandimento.
3. Irregolarità: il frattale non può essere descritto come luogo dei punti che soddisfano semplici condizioni geometriche o analitiche.

F non si può descrivere come luogo di punti che soddisfano semplici condizioni geometriche o analitiche, in quanto è una funzione ricorsiva nell’insieme dei numeri complessi.

4. Dimensione non intera: sebbene un frattale possa essere rappresentato in uno spazio convenzionale a due o tre dimensioni, la sua dimensione non è intera. In generale, un insieme composto da m copie di se stesso scalate di un fattore r avrà dimensione pari a log m/log r (nell’esempio riportato sopra la dimensione è log 4/log 3; per insiemi più complessi si devono adottare altre nozioni di dimensione. = 1,2618)

La caratteristica di queste immagini, caratteristica dalla quale deriva il loro nome, è che, sebbene esse possano essere rappresentate (se non si pretende di rappresentare infinite iterazioni, cioè trasformazioni per le quali si conserva il particolare motivo geometrico) in uno spazio convenzionale a due o tre dimensioni, la loro dimensione non è intera. In effetti la lunghezza di un frattale “piano” non può essere misurata definitamente, ma dipende strettamente dal numero di iterazioni al quale si sottopone la figura iniziale.

La storia dei Frattali

I frattali hanno una storia relativamente recente che coincide con l’avvento dell’elaborazione grafica computerizzata.

Il padre della teoria dei frattali è considerato Benoit Mandelbrot, che nel 1975 per primo formalizzò le proprietà di queste immagini che fino a quel momento erano considerate “mostri matematici”.

Il termine frattale venne coniato da Mandelbrot stesso nel libro “Les Objects Fractals: Forme, Hazard et Dimension” per descrivere alcuni comportamenti matematici che sembravano essere “caotici”, e deriva dal latino fractus (rotto, spezzato), così come il termine frazione; infatti, come già detto, le immagini frattali sono considerate dalla matematica oggetti di dimensione anche non intera.

Diversi frattali classici sono stati descritti da celebri matematici del passato, come Cantor, Peano, Hilbert, Von Koch, Sierpinski, ma solo con “The fractal geometry of nature” Mandelbrot li ha collocati in una teoria unificata, che ne sottolinea i legami con forme tipiche della natura.

Infatti i frattali non sono oggetti così astratti e lontani dalla vita quotidiana: ogni giorno ciascuno di noi si imbatte in qualcosa di molto simile ad un frattale come ad esempio alcuni tipi di foglie o di piante (i pini montani per esempio: dal tronco partono dei rami da cui partono altri rami ecc. ecc., per finire con gli aghi di pino), il profilo di un paesaggio roccioso (se non ci sono punti di riferimento, quali ad esempio una persona, è difficile stabilire quali siano le dimensioni reali di una roccia in una fotografia) oppure il “frattale” per eccellenza: il fiocco di neve che se osservato al microscopio rivela la sua struttura quasi frattale.

Il concetto matematico

La nozione di insieme frattale è strettamente legata al concetto di “dimensione” di un insieme.

Agli oggetti geometrici che ci sono familiari (retta, circonferenza, piano, superficie di una sfera, cubo ecc.) siamo in grado di associare la “dimensione” che li caratterizza: la retta e la circonferenza hanno dimensione 1, mentre il piano e la superficie della sfera hanno dimensione due; il cubo, in quanto oggetto solido, ha dimensione tre e il punto ha dimensione zero. In tutti questi casi la dimensione è un numero intero.

I frattali, come è stato spiegato sopra, sono al contrario esempi di insiemi di dimensione non intera perché hanno una struttura geometrica così complicata e lontana dalla semplicità degli insiemi considerati prima, da non permettere di attribuire loro una dimensione “intera”

La costruzione dei frattali si basa su un algoritmo di calcolo della velocità di convergenza di una funzione. Ciò significa che si è in presenza di un metodo, non necessariamente numerico, che deve essere utilizzato per disegnare l’immagine.

Questo algoritmo non è mai applicato una volta sola, ma è iterato un numero di volte teoricamente infinito: ad ogni iterazione, la curva si avvicina sempre più al risultato finale per approssimazione e, dopo un certo numero di iterazioni, l’occhio umano non è più in grado di distinguere le modifiche e anche l’hardware del computer non è più in grado di consentire ulteriori miglioramenti.

Pertanto, quando si disegna concretamente un frattale, ci si può fermare dopo un congruo numero di iterazioni.

L’algoritmo di Mandelbrot

I modelli matematici che danno origine ai Frattali sono molteplici, possono avere grandi complessità e possono essere ulteriormente arricchiti tramite meccanismi di traslazione e rotazione delle immagini di base originate (ad esempio i Frattali IFS).

Il Frattale più noto e più utilizzato è quello di Mandelbrot. Si basa su una formula matematica estremamente semplice che viene applicata al dominio dei numeri complessi²:

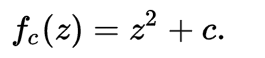
Con c parametro complesso.

L’incognita è indicata con z perché questa è la lettera che usualmente i matematici usano per i numeri complessi, invece della tradizionale x reale.

Questa funzione in analisi matematica è semplicemente una parabola traslata rispetto all’origine di un termine noto c complesso.

In questo modo il frattale di Mandelbrot è definito in un piano semicomplesso in cui i due assi sono rispettivamente per la parte reale ed immaginaria dei numeri.

  (cliccare immagine per miglior risoluzione)

L’insieme di Mandelbrot M, rappresentato in nero nell’immagine precedente, è definito a partire da una famiglia di polinomi quadratici complessi:

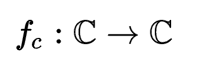
per ogni c del piano si considera il comportamento della successione:

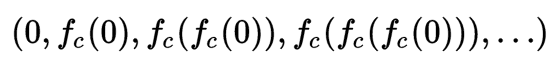
ottenuta iterando f a partire dal punto z=0.

L’elemento chiave dell’algoritmo è capire se questa successione è caratterizzata dal divergere all’infinito oppure essere limitata.

L’insieme M di Mandelbrot è definito come l’insieme dei punti c del piano tali che la corrispondente successione è limitata.

Una rappresentazione grafica rigorosa dell’insieme di Mandelbrot si ottiene colorando tutti i punti  che appartengono a M di nero e gli altri di un colore diverso.

Mandelbrot Zoom 10^227 - video

Le immagini multicolori che si vedono sono generate colorando i punti esterni all’insieme di Mandelbrot in base a “quanto velocemente” la sequenza f diverge all’infinito.

Per determinare l’appartenenza di un punto c a M, sequenza limitata, oppure in alternativa la velocità di divergenza dalla sequenza  f è sufficiente notare che nella formula di Mandelbrot compare il quadrato di z e quindi:

• Per la proprietà dei numeri complessi secondo la quale se un numero z ha modulo >=2, il suo quadrato, nella iterazione successiva, avrà modulo ancora maggiore e quindi, in cascata, la successione sarà divergente.
• Se invece la successione, dopo un certo numero massimo di iterazioni, non accenna a divergere (il numero z ha modulo < 2) si dà per scontato che non divergerà mai, e si accetta il punto che la origina come membro dell’insieme M.

Questo approccio non è matematicamente corretto dal punto di vista teorico, ma, se il numero di iterazioni è abbastanza alto, la probabilità di commettere errori di attribuzione è ragionevolmente limitata.

  (cliccare immagine per miglior risoluzione)

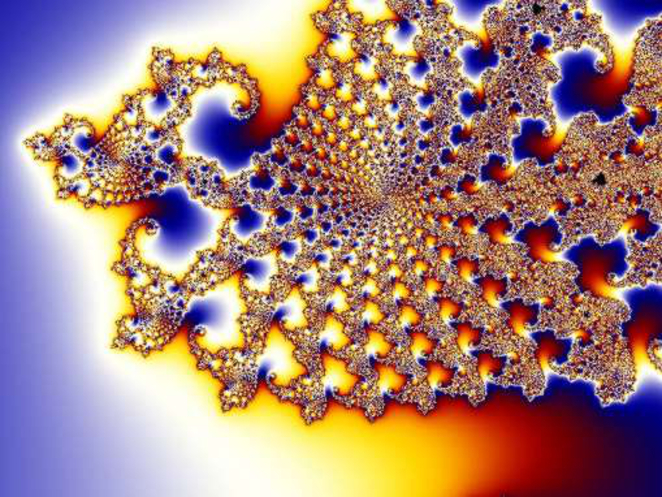
Paradossalmente, i punti colorati che conferiscono il fascino al frattale di Mandelbrot sono proprio quelli che non appartengono all’insieme M.

Per quanto detto finora, l’algoritmo di Mandelbrot opera nel seguente modo: viene calcolato ripetutamente il valore di z mediante la formula sopra indicata, e, ogni volta, il modulo di z viene confrontato col valore 2.

Il procedimento si arresta quando la successione mostra di essere divergente (mod(z)>=2) oppure quando si giunge al numero massimo di iterazioni che è stato preimpostato per definire la non divergenza.

Per ogni punto del piano di Mandlebrot, .si  indicano con colori diversi le velocità con cui la successione diverge: ad esempio, si colorano in blu i punti in cui la successione diverge alla prima iterazione, in verde quelli in cui diverge alla seconda, ecc.

Questo permette di ottenere favolose immagini:

  (cliccare immagine per miglior risoluzione)

L

Documentario sul set di Mandelbrot ( ≈ 21 min.)

matematica del caos: i Frattali

Ringraziamo tutti i numerosi lettori di Modus, che con la loro attenzione regolare o sporadica danno senso al nostro lavoro.
A quelli che gradirebbero essere informati sulle nostre pubblicazioni in tempo reale, e hanno un profilo attivo su Facebook, consigliamo di mettere il like sulla fan page: riceveranno senza dover fare l’accesso al sito il link di tutti i nuovi articoli.

La redazione