Elogio dei numeri primi

Molti di noi utilizzano il web per comunicare e, ancor più temerariamente, per trasmettere documenti importanti e riservati, per dialogare con la propria banca, per acquistare prodotti. Forse non tutti sanno che la nostra “segretezza” in internet, sia quando scriviamo alla fidanzata di turno, sia quando acquistiamo le Hogan a prezzo scontatissimo (sic!), digitando il numero della nostra carta di credito, è legata a secoli di Storia della Matematica. Il tema in questione è quello della “cifratura”, della “criptazione dell’informazione”. L’obiettivo e quello di rendere incomprensibile il messaggio che si trasmette ad eccezione del legittimo destinatario. Il tema della “crittografia” di cui la tecnica militare fece (e continua a fare, in modo sempre più sofisticato) uso in passato, investe nei tempi attuali tutti i campi di utilizzo dei sistemi informatici. Plutarco ne “Le vite parallele” ci racconta che a Sparta, 2500 anni fa, i magistrati, controllori dei re e in contatto continuo con i generali, trasmettevano i loro messaggi importanti e riservatissimi con questo metodo: mittente e destinatario impiegavano due bastoni di legno cilindrici perfettamente identici (stesso diametro e lunghezza); il mittente avvolgeva a spirale un sottile nastro di pergamena, lungo e stretto, intorno al proprio bastone. Successivamente scriveva il proprio messaggio in righe longitudinali. Quando la pergamena veniva srotolata il testo del messaggio appariva privo di senso e riacquistava significato solo se riavvolta intorno al bastone gemello che era posseduto solo dal legittimo destinatario. Altri esempi si potrebbero fare. Successivamente, intorno agli anni settanta, del secolo trascorso, le tecniche si affinarono e si introdusse il concetto di “chiave pubblica” e “chiave privata”. Esistono due chiavi, una segreta ed una pubblica: chiunque può adottare la chiave pubblica per criptare un messaggio, ma solo il proprietario della chiave segreta sarà in grado di leggerne il contenuto. Cioè, mentre nella crittografia simmetrica la chiave è unica, in quella asimmetrica le chiavi sono due: per criptare un messaggio si usa un algoritmo controllato da una chiave di codifica detta pubblica, ma per decodificarlo si usa un algoritmo connesso al primo che però è controllato da una chiave detta privata. Simon Sing, autore di un testo sull’ultimo teorema di Fermat (ecco il nome emblematico che ci apre la finestra sulla teoria dei numeri…), bene illustra questo concetto con questa frase: ““La crittografia asimmetrica potrebbe essere illustrata nel modo seguente: chiunque può chiudere un lucchetto facendo scattare l’anello metallico, ma solo chi ha la chiave può aprirlo. La chiusura è alla portata di tutti (come la cifratura) ma l’apertura è privata (come la decifrazione) e possibile solo per il possessore della chiave”. 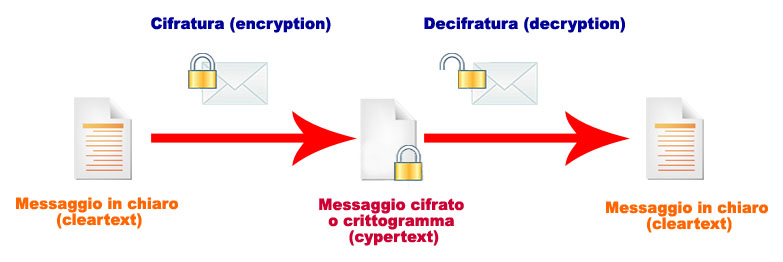  Un classico esempio è il commercio elettronico: il responsabile di un’attività commerciale, che vende i suoi prodotti su Internet, fornisce ai suoi clienti la chiave pubblica con cui possono crittografare (con opportuni software, lo facciamo senza rendercene conto…) il numero della propria carta di credito. A questo punto, il messaggio criptato può essere decodificato solo da chi gestisce il commercio, in quanto solo lui e, nessun altro, possiede la chiave privata. Quindi, se anche una terza persona venisse indebitamente in possesso dei numeri, ormai criptati, non potrebbe farne uso, perché non conosce la chiave per decifrarli. Si va bene, ma i numeri primi? Al tempo… Uno degli algoritmi asimmetrici di cifratura più conosciuti è l’algoritmo RSA, acronimo formato dalla prima lettera dei cognomi di coloro che lo inventarono nell’aprile del 1977: Ronald L. Rivest, Adi Shamir e Leonard M. Adleman. Le due chiavi possono essere ricavate l’una dall’altra, ma la garanzia fornita da RSA è che l’operazione di derivare la chiave segreta da quella pubblica è troppo complessa per venire eseguita in pratica, anche su un calcolatore molto potente; infatti, RSA sfrutta il fatto che è facile calcolare il prodotto di due numeri primi anche molto grandi, ma dato un numero è molto più difficile scomporlo, cioè trovare i numeri primi il cui prodotto è proprio il numero dato. Eccoli, dunque, arrivano i protagonisti della matematica: sono i numeri primi. Ricordiamo che un numero naturale (cioè intero e maggiore di zero), diverso da uno, è primo se è divisibile solo per uno e per se stesso. Quindi, 2 è primo (è l’unico pari ad esserlo), 3, 5, 7, 11, ecc, sono primi. I numeri primi rappresentano uno dei misteri più affascinanti della scienza. Generazioni di matematici hanno lavorato per risolvere vari quesiti relativi a quelli che Marcus du Sautoy definisce “il ritmo cardiaco, irregolare, della matematica”.  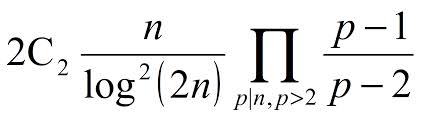 Se conosciamo tutti i numeri primi fino a un certo numero, possiamo prevedere quale sarà il prossimo? C’è una formula capace di generare numeri primi? Eratostene, Euclide, Mersenne, Fermat, Goldbach, Euler, Gauss etc. etc fino al grandissimo Riemann, hanno speso tutte le loro energie mentali intorno a questo tema.   Du Sautoy, docente di matematica all’Università di Oxford – uno dei maggiori specialisti mondiali di teoria dei numeri, autore de “L’enigma dei numeri primi – L’ipotesi di Riemann, l’ultimo grande mistero della matematica” dove affronta molto a fondo la questione – afferma che i numeri primi sono il cardine della matematica per il quale, nel corso dei secoli, molti studiosi hanno elaborato teorie. Teorie volte a 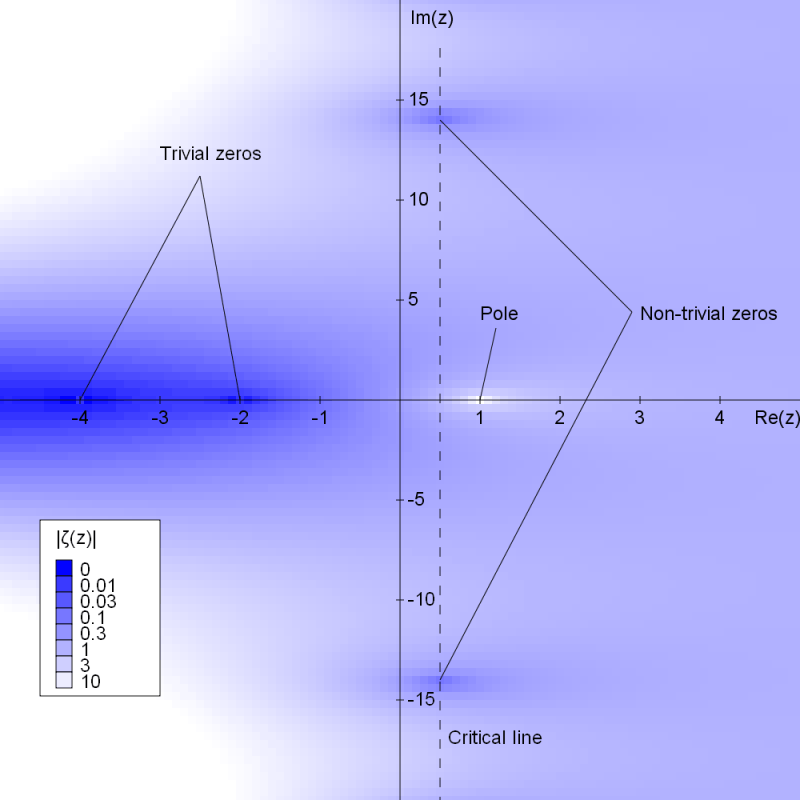dimostrare l’esistenza o meno di un ordine nella sequenza, apparentemente caotica, di questi particolari numeri o la possibilità di trovare una formula o una regola che permettesse di stabilire qual è, per esempio, l’ennesimo numero primo. Bernhard Riemann, matematico e fisico tedesco nato a Breselenz il 17 settembre 1826 e morto a Selasca il 20 giugno 1866, elaborò un’ipotesi, nota appunto come ipotesi di Riemann, che Hilbert, uno dei più grandi matematici dell’epoca, inserì all’ottavo posto tra i famosi ventitré problemi (tra questi anche il teorema di Fermat), e che presentò, nell’agosto del 1900, al Congresso internazionale dei matematici alla Sorbona di Parigi. L’ipotesi non fu né dimostrata, né confutata per tutto il ventesimo secolo ed è ora considerata tra i sette più difficili problemi del nuovo millennio: nel 2000 il Clay Mathematics Institute ha offerto un premio di un milione di dollari a chi riuscirà a provarli, ma stranamente non ha offerto nessun premio a chi ne dimostrasse la falsità. Attualmente, tramite l’uso di computer, si è calcolato che, per il primo miliardo e mezzo di numeri primi (si avete lette bene: il primo miliardo e mezzo!) l’ipotesi è vera: per la matematica, però, ciò non è sufficiente. Infatti basterebbe un solo contro esempio perché l’ipotesi fosse assolutamente falsa. Una cosa e certa: Riemann ha lasciato ai matematici l’arduo compito di dimostrare che l’ordine che regolava il mondo dei numeri primi, da lui ipotizzato, esisteva effettivamente. La dimostrazione dell’ipotesi di Riemann avrebbe importanti conseguenze, sconvolgenti per tutta la scienza matematica. per esempio, molti teoremi che iniziano con “ …supponendo che l’ipotesi di Riemann sia esatta… ”, sarebbero automaticamente veri. E, tornando alle origine dei protagonisti solitari, imprevedibili e occulti dei nostri “movimenti nella rete”, si aprirebbero poi nuove strade per la comprensione della struttura dei numeri primi, si avrebbe inoltre, forse, la possibilità di trovare un criterio per scomporre un numero in fattori primi molto più rapido di quelli attuali e, come afferma Du Sautoy, ciò “ metterebbe in ginocchio l’intero commercio elettronico nello spazio di una notte ”.